こんにちわあひるです🐤
前回の記事では「宝くじがいかに当たらないか」を、バスケットコートに落ちる目薬に例えてお話ししました。
-

-
【あなたは大丈夫?】情弱が大好きな宝くじ̩/買うだけ損な3つの理由
こんにちわAGEです🐤 年末になると宝くじの季節になってきます。 少し前まで私も「ちょっとだけなら」と言う気持ちで毎年1万円分購入していました。 そんな宝くじ、テレビCMを流し"夢"を語っていますが、 ...
続きを見る
そんな中、驚きのニュースが飛び込んできました。
投資家グループが3,600万円かけて12万枚の年末ジャンボを共同購入したというのです。
「12万枚も買えば、さすがに1等に手が届くのでは?」
「億トレーダーたちが集まれば、運気で確率を超えられるのでは?」
今回は、このプロジェクトの結果を統計学的にシミュレーションし、大量購入の裏に潜む「大数の法則」の残酷な真実を暴いていきたいと思います。
この記事の結論
宝くじは「たくさん買えば当たる」のではなく、「たくさん買うほど理論通りの負けに近づく」という数学・統計学的な罠があります。夢を見るなら、枚数ではなく「運」に賭けて少額で楽しむのが正解です。
それでは、Let's go!!
1. 衝撃の結果:3,600万円が「1,000万円」に
ニュースで報じられた「年末ジャンボ11万9,975枚」の購入結果を、前回の還元率と照らし合わせてみましょう。
| 項目 | 今回のリアルな結果 | 理論上の数値(還元率46%) |
| 投資額(購入額) | 35,992,500円 | 35,992,500円 |
| 当選金額(回収額) | 10,579,800円 | 約1,673万円 |
| 収支 | 約2,541万円の赤字 | - |
| 今回の還元率 | 約29.4% | 46.5% |

そうなんです。理論上の還元率(46.5%)すら大きく下回る結果となりました。
実は、大量購入には「逃げ場のない数学の罠」が仕掛けられているのです。
2. 大量の購入は「負け」を確定させる作業?(大数の法則)
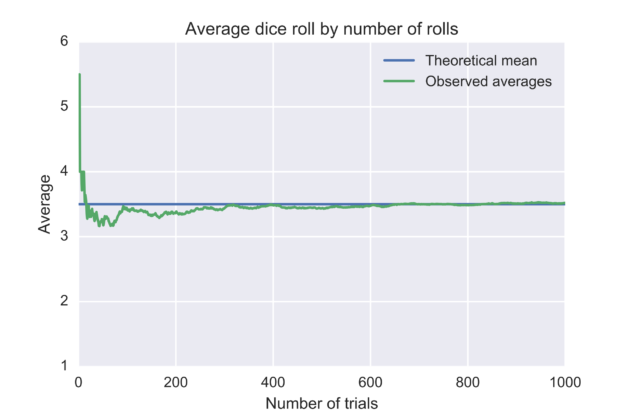
ここで重要なのが「大数の法則」という考え方です。
簡単に言うと、「試行回数(買う枚数)を増やすほど、結果は理論上の平均値に近づく」という法則です。
<出典:Wikipedia>
大数の法則を分かりやすくイメージ
-
数枚だけ買う時: 運が良ければ還元率が数万倍になる「ブレ」がある。
- 数万枚買う時: 運の要素が削ぎ落とされ、「国に53%抜かれる」という現実がどんどん確定していく。
今回の共同購入では、枚数を増やしたことで「全ハズレ」という最悪の事態は避けられましたが、同時に「買えば買うほど、計算通りの負けに収束していく」という統計学の正しさを証明する形になりました。
3. 統計シミュレーション:12万枚で1等は当たるのか?
「12万枚も買ったなら、1等7億円にかなり近づいたのでは?」と思うかもしれません。
しかし、現実は非常に厳しいものです。
前回の例えを覚えていますか?
1等の確率は「バスケットコート10面分のエリアに滴下される目薬を、自分の目で受ける確率」でした。
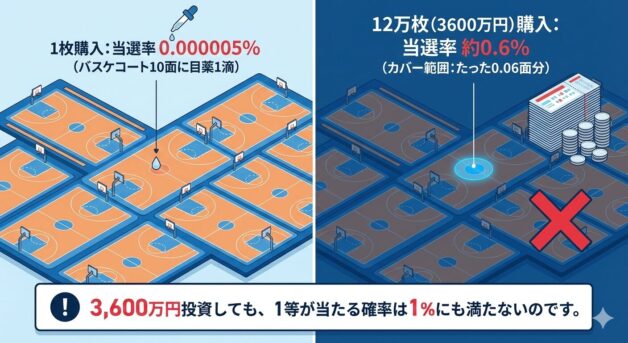
- 1枚買った時の当選率: 0.000005%
- 12万枚買った時の当選率: 約0.6%
3,600万円投資しても、1等が当たる確率は1%にも満たない(0.6%)のです。
12万枚という数字は圧倒的に見えますが、ターゲット(1等)に対しては、バスケットコート10面のうち、たった0.06面分をカバーしたに過ぎません。残りの9.94面分に落ちたら即終了です。
4. まとめ:300円で「夢」を、3,600万円で「教育」を
今回の共同購入の主催者は、このように語っています。
「購入から当選発表までの1カ月間、『当たったらどうしよう』と高揚感は高く、これを300円から味わえるのは最強です。メンタル的にはプラスです。」
これは非常に健全な楽しみ方だと言えます。
宝くじは資産形成ではなく、「大損することを承知の上で、ワクワクする時間を買う娯楽」だからです。
今回の教訓
-
1枚買う人: 300円で「1ヶ月の夢」を買う(安い!)
- 12万枚買う人: 3,600万円で「大数の法則」を証明する(高い!)
もしあなたが本当に資産を増やしたいのであれば、大数の法則を味方につけて「期待値が100%を超えるもの(投資)」に資金を投じるべきでしょう。

資産形成は計画的に。
それでわ。