こんにちは、あひる（Twitter）です。
今回はこういった疑問に答えます。
先に流れを言ってしまうと、『求人情報から必要な情報（年収）を抽出して、その情報を元に統計学を使用して算出』しています。
それでは、Let's go!!
ネットの情報
まずネットの情報を確認すると、、、
・データサイエンティスト（以降DS）の平均年収は650万円
・一般会社員の平均年収は420万円
一般会社員と比較するとかなり高額です。
「年収が高い＝需要がある」とも読み取れますので、まだ魅力ある業種の１つだと思われます。
ネットの情報を鵜呑みにしてはいけませんので、その平均年収を自分の手で確認していきたいと思います。
求人情報をスクレイピング
冒頭にも説明させてもらいましたが、流れとしては『求人情報から必要な情報（年収）を抽出して、その情報を元に統計学を使用して算出』です。
『抽出＝スクレピング』となります。
今回はdodaさんのサイトからDS案件に絞り、Pythonで必要な情報だけをスクレイピングしていきました。
私が調査したタイミングでは該当求人数が1,126件でしたが、日によって変わりますので今回の結果は私が調査したタイミングでの結果という事にご注意ください。
又、サイトによってはスクレイピングを禁止されていることもありますので利用規約や禁止事項の確認をお願いします。
Pythonくんが頑張って1,126件分の会社名、URL、従業員数、年収をスクレイピングしてきてくれました。
分析しやすいように加工して、このステップは完了です。
母平均の区間推定を行う
データ準備
まずは必要なライブラリーとデータを取り込みます。
Python
import pandas as pd
from sklearn.datasets import load_boston
from datetime import datetime, timedelta
df = pd.read_csv("data_science_company_list - data_science_company_list.csv", index_col=[0])
df.head()
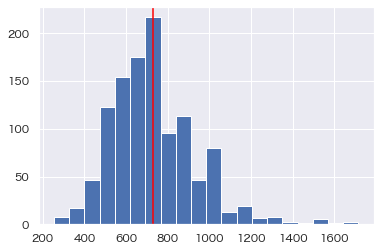
"年収"の分布を確認。
Python
import matplotlib.pyplot as plt
data = df["年収"]
#平均
mean = df["年収"].mean()
plt.axvline(x=mean, color="red")
plt.hist(data, bins=20)
正規分布に近い形ですかね。
中心極限定理により母集団の分布によらず、標本サイズが大きい場合、平均の標本分布は正規分布とする
今回は n=1,126 なのでOKとします。中心極限定理恐るべし・・・
95%信頼区間を求める
ここから95%信頼区間を求めていきますが、その意味とは「母集団から取り出した標本の平均から95%信頼区間を求める作業を100回繰り返した時に、95回はその区間に母平均が含まれる」事となります。
つまり95%信頼区間は確率ではなく、割合を表しています。
参考サイト：統計WEB_95%信頼区間のもつ意味
まずは必要なパラーメータを求めます。
Python
#不偏分散
var = df["年収"].var()
#自由度
deg_of_freedom = len(df["年収"])-1
#標準偏差（統計量tの分母）
scale = math.sqrt(var/len(df["年収"]))
次にt分布を用いた区間推定を行います。
Python
from scipy.stats import t
#信頼区間の%、自由度、標本平均、標本の標準偏差
bottom, up = t.interval(0.95, deg_of_freedom, loc=mea, scale=scale)
print(bottom)
print(up)
>>717.8240006662061
>>741.7143253249833
つまり、95%信頼区間は「717万円 ≦ μ ≦ 742万円」という結果となりました。
ネット情報だとDSの平均年収は650万円でしたので、さらに高額となりました。
まとめ
・求人サイトからDSの平均年収を算出
・一般の平均年収より高い＝需要があると推測
・プログラミングを勉強すると自分で出来ることが広がるのでオススメです